Trie
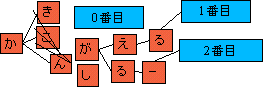
Trie を用いた単語の特定方法
Indexの実現方法として、Trie構造があげられる。。 Trie構造は図R−1のような構造のことであり、 単語を文字に分解して木構造になるようにデータを結合したものである。 例えば、”かき”,”かこ”、”かん”,”かんがえる”、”かんがるー”、”かんし”という単語を元に 作成すると図R−1ようなTrieが出来る。Trieは一文字選択するごとに、選択肢を限定していけることから 高速に処理することができることがわかると思う。
しかし、後日説明するが、Trieは大きなデータ構造であるために、特別な処理が必要です。 極めてデータが大きくなると、ハードディスクからアクセスすることになり、 とても重い処理になってしまいます。そこで圧縮を行ってあげたり、ハードディスクからの読み込みを あまり意識しなくて良いようにする必要があります。
(Modern nformation retrival は Tree や 圧縮関連の知識が集められているので必読ですよ!!)
圧縮を行うにしても、ハードに保存するにしても、整列化する必要があります。 一度整列化すると、 Trieを再構成するのが難しくなるので、整列化したTrieをこのページでは 静的なTrieと呼ぶことにします。 (なぜかは後で、解決策も後で)
木構造を無駄なく、深さ優先で保存する方法について説明を行います。
深さ優先データを保存する
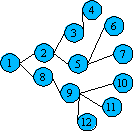
深さを優先して保存する場合らは木構造は図Trie−1のよ数字が示すような順番でデータを保存していく。 深さ優先でデータを保存する場合は、メモリーに下位の木構造ごと一括で一括でよみとることができる。例えば、1以下の下位構造すべてを読み取る場合には、1から12までのデータを読みとることであり。2以下の下位構造2から7までのデータをメモリーに読み取ることを意味している。これらの機能は、ハードディスクのSeekの回数を減らすことができるため、複数のアプリレーションでハードを共有している場合に、より早く処理することができ可能性がある 。ハードディスクがseekする範囲が大きくなると。その分時間を必要とするためである。
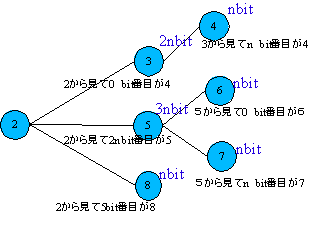
深さ優先の場合ポインタ分だけ重くなる
葉の位置を知っておくことで、探索回数ほ減らすことが出来る。 木が葉の位置を知らない場合、例えば2から8へ移るには、3 4 5 6 7というステップを踏まなくては成らない。これは非効率である。そこで、2は3と5と8の位置をあらかじめ知っていれば、 3 4 5 6 7というステップを踏まなくて良くなるわけである。葉の位置は図Trie−2のように配置する方法が考えられる。一つのノードが必要にとする容量がnbitの時、親ノードは子ノードの容量とnbitを足した数()だけ必要となる。 これらのノードに必要となる容量を参考にリンク表を作ると。 最低でも リンク数×ポインターの大きさのだけTrieは大きな構造になるのである。