これからの予定
3D環境をMingで使えるようにする。ただし
既存のものはなるべく使わないようにすることにしよう。
(既存のものはREDHOT PEPPER JP)が参考になります
そうすれば、3Dグラフィックの原理だとかが少しはわかってくるかも知れない。
今回こんなことをはじめようと思ったのはGUMOB.COMでの
3Dのリンクを見て作れそうだと思ったことと、
いちどMingを用いてすこし複数のMovieClipを必要とするようなものを作成してみたかったからです。
、
今日行ったこと
考えたこと
四元数なんてものもあるようですが、3D環境を表示しようと考えたとき、一番最初に私の脳をよぎったのは
やはり行列と極座標表示でした。四元数はとてもすばらしいもののようですが、現在の私が考えしなかったことに
挑戦するのは問題があると考えました。今月は行列を用いて座標変換をこまごますることにします。
極座標
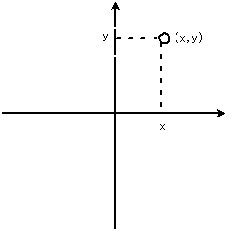
そもそも極座標とは何なのでしょうか。皆さんは座標というものはご存知ですね。
座標を用いる(x,y)で座標上の位置をあらわすことがきます。xが横軸、yが縦軸といった具合です。
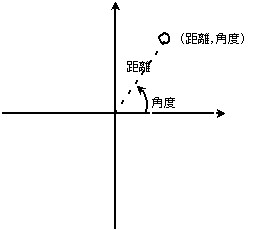
極座標は原点から目的地までの長さと、その角度で座標上の位置を表します。(距離,角度)といった具合です
極座標から座標へ
極座標から座標へ変換するには。直角三角形というものが
角度と長さを指定することで、直角三角形の形を指定できると
いうことを用います。
直角三角形の角度と長さから頂点座標を求めることは
計算することではできません。
ただし、長さと角度を指定することで直角三角形を書くことができるわけですから
確かに、頂点座標は存在するのです。
そこで過去の偉人たちは角度によって座標の位置がどこに移動するかを調べたのです。
しかし、現在、私たちはあまり深く考えることなく角度から座標を求めることができます。
これらの角度と座標との関係を調べていった結果を辞書のように保存してくれているものがあるからです。
それはcosだとかsinだとかといったものです。
sin cos
(x,y)は(距離×cos(角度),距離×sin(角度))と書くことができます。
Mingでしたこと
ためしに二次元での座標変換を行ってみることにしました。
回転
(x,y)座標上の点を原点を中心に回転した後の点を(_x,_y)としたとき
_x = x×cos(角度)+y×sin(角度)
_y = x×sin(角度)+y×cos(角度)
と表すことができます。
移動
(x,y)座標上の点を移動した後の点を(_x,_y)としたとき
_x = x+x軸に平行に移動する距離
_y = y+y軸に平行に移動する距離
拡大
(x,y)座標上の点を原点を中心に拡大した後の点を(_x,_y)としたとき
_x = x×拡大率
_y = y×拡大率
座標変換する
表示してみる
?
こんなのができます
うーん、繰り返し座標変換すると大きさの情報に
誤差が生まれていますね。
これらをふまえて、次は行列に挑戦してみることにしましょう。

